slope singularity in modified Veloclinic model: reassessing the aerobic component
Previously I fit a 2-component "modified Veloclinic" model to some of my old power-duration data. This worked fairly well, but sprinting power was almost universally overestimated. Experimentally there was a sharper transition from time-dependent power to peak sprint power.
The thing is I don't see this in Veloclinic's fits. Nor do I see it in the Damien's Gauser's enhanced model in Golden Cheetah 3.1 development version, which is curious. So what's the problem?
Well, one difference is I embraced the strictly heuristic modification of the aerobic term with an α term:
Paerobic = P2 ( τ2 / t)α2 ( 1 - exp[ -( t / τ2)α2 ] )
Where I observed that for this term α = 1/2 worked nicely. So I decided to go with that as a constant, and not fit it to the models. I got better fits to the long-time data than I see with Veloclinic's model, which has α = 1 for all components. The rationale is that aerobic power isn't fixed capacity, but has essentially unlimited capacity with diminishing returns.
I want to examine this more closely. For long times, the exponential becomes small, the 1 dominates, and you get:
Paerobic → P2 ( τ2 / t )α2
This seems reasonable, and was justification for this ad hoc adjustment.
But what about short times? At times t ≪ τ2, the exponential is close to 1, and I can use the Taylor-series expansion for exponential:
exp[-x] = 1 - x ( 1 - ½ x ( 1 - 1/3 x ( 1 - 1/4 x ( ... ) ) ) )
Considering values only out to order x2, I get the following for the function:
Paerobic → P2 (τ2 / t)α2 ( 1 - 1 + (t / τ1)α2 - ½ (t / τ2)2α2 ...)
Simplifying this yields:
Paerobic → P2 (1 - ½ (t / τ2)α2 ...)
This starts at P2 and decreases, as expected. But consider the derivative:
∂ Paerobic/∂ t → -½ P2 α2 (t / τ2)α2 - 1 ...
For α2 = ½, the derivative has a time dependence of 1 / sqrt(time) for small times: that's a singularity.
So while the gradual decay of this function at long times is attractive, its behavior for short times is suspicious.
Here is a comparison of fits with the two versions, the original with α2 = 1, and my modified form with α2 = ½:
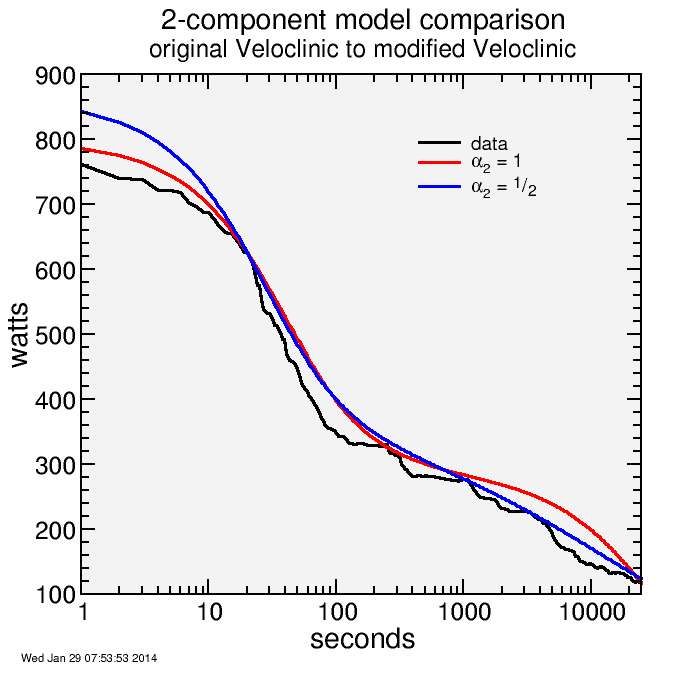
For long times, the blue curve fits much better, supporting the α2 = ½ form, but for short times the α2 = 1 curve does much better. In between I'll call it a wash.
This suggests that a better form is needed for the aerobic power: one which has the gradual decay at long times of the α2 = ½ curve, yet which at short times saturates to P2 more definitively, similar to the α1 = 1 curve. And a slope singularity at t → 0 simply won't do. That's aesthetically offensive if nothing else.
There are constraints on this function. For example, it can fall off with time no quicker than 1/time: the derivative of the logarithm of the function with respect to the logarithm of time must be between 0 and -1, inclusive. An exponential, which is a very attractive function from its scaling properties, fails this test. It would result in work capacity decreasing over time for long time durations, and that's impossible. Another constraint on the function is it should be simple. For example, a rational polynominial function with 4 coefficients isn't so good. Nor is something which can't readily be analytically differentiated (needed for the Jacobian matrix).
An example of a function which starts out flat then decays with a power-law dependence is the following:
f = 1 / [ 1 + (t / τ)]α
I'll look more into this option next time.
Comments